import geopandas as gpd
import esda
import matplotlib.pyplot as plt
import seaborn as sns
from libpysal import graphSpatial autocorrelation
In the last section, you learned how to encode spatial relationships between geometries into weights matrices represented by Graph objects and started touching on spatial autocorrelation with spatial lag and Moran plot. This section explores spatial autocorrelation further in its global and local variants.
Spatial autocorrelation has to do with the degree to which the similarity in values between observations in a dataset is related to the similarity in locations of such observations. Not completely unlike the traditional correlation between two variables -which informs us about how the values in one variable change as a function of those in the other- and analogous to its time-series counterpart -which relates the value of a variable at a given point in time with those in previous periods-, spatial autocorrelation relates the value of the variable of interest in a given location with values of the same variable in surrounding locations.
A key idea in this context is that of spatial randomness: a situation in which the location of observation gives no information whatsoever about its value. In other words, a variable is spatially random if it is distributed following no discernible pattern over space. Spatial autocorrelation can thus be formally defined as the “absence of spatial randomness”, which gives room for two main classes of autocorrelation, similar to the traditional case: positive spatial autocorrelation, when similar values tend to group together in similar locations; and negative spatial autocorrelation, in cases where similar values tend to be dispersed and further apart from each other.
In this session, you will learn how to explore spatial autocorrelation in a given dataset, interrogating the data about its presence, nature, and strength. To do this, you will use a set of tools collectively known as Exploratory Spatial Data Analysis (ESDA), specifically designed for this purpose. The range of ESDA methods is very wide and spans from less sophisticated approaches like choropleths and general table querying to more advanced and robust methodologies that include statistical inference and explicit recognition of the geographical dimension of the data. The purpose of this session is to dip your toes into the latter group.
ESDA techniques are usually divided into two main groups: tools to analyse global, and local spatial autocorrelation. The former considers the overall trend that the location of values follows and makes possible statements about the degree of clustering in the dataset. Do values generally follow a particular pattern in their geographical distribution? Are similar values closer to other similar values than you would expect from pure chance? These are some of the questions that tools for global spatial autocorrelation allow to answer. You will practice with global spatial autocorrelation on the Join Counts statistic and Moran’s \(I\) statistic.
Tools for local spatial autocorrelation instead focus on spatial instability: the departure of parts of a map from the general trend. The idea here is that, even though there is a given trend for the data in terms of the nature and strength of spatial association, some particular areas can diverge quite substantially from the general pattern. Regardless of the overall degree of concentration in the values, you can observe pockets of unusually high (low) values close to other high (low) values in what you will call hot (cold) spots. Additionally, it is also possible to observe some high (low) values surrounded by low (high) values, and you will name these “spatial outliers”. The main technique you will review in this session to explore local spatial autocorrelation is the Local Indicators of Spatial Association (LISA).
Data
For this session, you will look at the election data. In particular, the results of the second round of the presidential elections in Czechia in 2023, between Petr Pavel and Andrej Babiš, on a level of municipalities. Each polygon has a percentage of votes for either of the candidates attached, as well as some additional information. Election data are provided by the Czech Statistical Office, and geometries are retrieved from ČÚZK. The dataset is preprocessed for the purpose of this course. If you want to see how the table was created, a notebook is available here.
To make things easier, you will read data from a file posted online, so you do not need to download any dataset:
- 1
- Use the name of each municipality as an index. It will help you link them to the weights matrix.
- 2
- Create a plot to explore the data.
- 3
-
"PetrPavel"is the name of the column with the proportions of votes for Petr Pavel. - 4
-
Use
"coolwarm"divergent colormap to distinguish between municipalities where Petr Pavel won and those where Andrej Babiš did. - 5
- Normalise the colormap between 0 and 100 to ensure that the split between blue and red is at 50%.
- 6
- With larger tables, using Canvas rendering instead of the default one is helpful.
- 7
- Use less intense background tiles than the default OpenStreetMap.
Instead of reading the file directly off the web, it is possible to download it manually, store it on your computer, and read it locally. To do that, you can follow these steps:
- Download the file by right-clicking on this link and saving the file
- Place the file in the same folder as the notebook where you intend to read it
- Replace the code in the cell above with:
elections = gpd.read_file(
"cz_elections_2023.gpkg",
)Spatial weights refresher
You already know how to work with the spatial weights matrices from the previous session. In this case, you will need to create queen contiguity weights, which consider two observations as neighbours if they share at least one point of their boundary. In other words, for a pair of municipalities in the dataset to be considered neighbours under this \(W\), they must be sharing borders or “touching” each other to some degree.
Technically speaking, you will approach building the contiguity matrix in the same way you did before. You will begin with a GeoDataFrame and pass it on to the queen contiguity weights builder in libpysal. You will also make sure your table of data is previously indexed on the municipality name, so the \(W\) is also indexed on that form.
1contiguity = graph.Graph.build_contiguity(elections, rook=False)- 1
-
Since the default would be Rook contiguity, you set
rook=False.
Now, the contiguity object you have is the same type as any other one you have created. As such, you can inspect it in the same way. For example, you can check who is a neighbour of observation Hrazany:
contiguity["Hrazany"]neighbor
Petrovice (Příbram, 541044) 1
Hrejkovice 1
Chyšky 1
Kovářov 1
Milevsko 1
Name: weight, dtype: int64Since you will be dealing with spatial lags, it may be wise to row-standardise the matrix.
contiguity_r = contiguity.transform("r")Now, because you have row-standardize them, the weight given to each of the five neighbours is 0.2, which equals one.
contiguity_r["Hrazany"]neighbor
Petrovice (Příbram, 541044) 0.2
Hrejkovice 0.2
Chyšky 0.2
Kovářov 0.2
Milevsko 0.2
Name: weight, dtype: float64Spatial lag refresher
You also know what spatial lag is. Once you have the data and the spatial weights matrix ready, you can start by computing the spatial lag of the percentage of votes that went to the winning candidate, Petr Pavel. Remember that the spatial lag is the product of the spatial weights matrix and a given variable. If \(W\) is row-standardized, the result amounts to the average value of the variable in the neighbourhood of each observation.
We can calculate the spatial lag for the variable "PetrPavel" and store it directly in the main table with the following line of code:
elections['PP_lag'] = contiguity_r.lag(elections["PetrPavel"])
elections.head()| nationalCode | PetrPavel | AndrejBabis | sourceOfName | geometry | PP_lag | |
|---|---|---|---|---|---|---|
| name | ||||||
| Želechovice nad Dřevnicí | 500011 | 61.73 | 38.26 | Český úřad zeměměřický a katastrální | MULTIPOLYGON (((-518835.63 -1170505.52, -51790... | 63.431667 |
| Petrov nad Desnou | 500020 | 49.07 | 50.92 | Český úřad zeměměřický a katastrální | MULTIPOLYGON (((-559207.18 -1075123.25, -55624... | 51.467500 |
| Libhošť | 500046 | 47.78 | 52.21 | Český úřad zeměměřický a katastrální | MULTIPOLYGON (((-486502.29 -1123694.06, -48717... | 54.154000 |
| Krhová | 500062 | 58.79 | 41.20 | Český úřad zeměměřický a katastrální | MULTIPOLYGON (((-494514.83 -1136457.23, -49539... | 57.782500 |
| Poličná | 500071 | 58.20 | 41.79 | Český úřad zeměměřický a katastrální | MULTIPOLYGON (((-499678.51 -1143457.52, -49799... | 54.198333 |
The way to interpret the spatial lag (PP_lag) for, say, the first observation is as follows: Abertamy, where Petr Pavel received 62.98%, is surrounded by neighbouring municipalities where, on average, more than 65% of the electorate also voted for him. For the purpose of illustration, you can, in fact, check this is correct by querying the spatial weights matrix to find out Abertamy’s neighbours:
contiguity_r['Abertamy']neighbor
Boží Dar 0.25
Jáchymov 0.25
Merklín (Karlovy Vary, 555363) 0.25
Pernink 0.25
Name: weight, dtype: float64And then checking their values:
neis = elections.loc[contiguity_r['Abertamy'].index, "PetrPavel"]
neisneighbor
Boží Dar 89.09
Jáchymov 53.88
Merklín (Karlovy Vary, 555363) 50.42
Pernink 68.85
Name: PetrPavel, dtype: float64And the average value, which you saw in the spatial lag is 65.56, can be calculated as follows:
neis.mean()np.float64(65.56)For some of the techniques you will see below, it makes more sense to operate with the standardised version of a variable rather than the raw one. Standardising means subtracting the average value and dividing it by the standard deviation.
\[ z_i = \dfrac{y - \bar{y}}{\sigma_y} \]
where \(z_i\) is the standardized version of \(y_i\), \(\bar{y}\) is the average of the variable, and \(\sigma\) its standard deviation.
This can be done easily with a bit of basic algebra in pandas:
elections["PP_std"] = (
elections["PetrPavel"] - elections["PetrPavel"].mean()
) / elections["PetrPavel"].std()Finally, to be able to explore the spatial patterns of the standardised values, also called sometimes \(z\) values, you need to create its spatial lag:
elections["PP_std_lag"] = contiguity_r.lag(elections["PP_std"])Global spatial autocorrelation
Spatial autocorrelation is measured differently depending on the type of data. For boolean (True or False) variables, you can use the Join Counts statistic, while for continuous variables, you can use Moran’s \(I\). Let’s start with the boolean case.
Join Counts for boolean variables
The elections dataset does not contain any boolean variable, but it is easy to create one representing whether Petr Pavel lost in a municipality or not.
1elections["PP_lost"] = (elections["PetrPavel"] < 50).astype(int)
elections.head()- 1
-
Get a mask with True and False values (
elections["PetrPavel"] > 50) and convert it to 1 and 0, which is what Join Counts expect.
| nationalCode | PetrPavel | AndrejBabis | sourceOfName | geometry | PP_lag | PP_std | PP_std_lag | PP_lost | |
|---|---|---|---|---|---|---|---|---|---|
| name | |||||||||
| Želechovice nad Dřevnicí | 500011 | 61.73 | 38.26 | Český úřad zeměměřický a katastrální | MULTIPOLYGON (((-518835.63 -1170505.52, -51790... | 63.431667 | 0.678189 | 0.826837 | 0 |
| Petrov nad Desnou | 500020 | 49.07 | 50.92 | Český úřad zeměměřický a katastrální | MULTIPOLYGON (((-559207.18 -1075123.25, -55624... | 51.467500 | -0.427720 | -0.218287 | 1 |
| Libhošť | 500046 | 47.78 | 52.21 | Český úřad zeměměřický a katastrální | MULTIPOLYGON (((-486502.29 -1123694.06, -48717... | 54.154000 | -0.540407 | 0.016391 | 1 |
| Krhová | 500062 | 58.79 | 41.20 | Český úřad zeměměřický a katastrální | MULTIPOLYGON (((-494514.83 -1136457.23, -49539... | 57.782500 | 0.421366 | 0.333357 | 0 |
| Poličná | 500071 | 58.20 | 41.79 | Český úřad zeměměřický a katastrální | MULTIPOLYGON (((-499678.51 -1143457.52, -49799... | 54.198333 | 0.369827 | 0.020263 | 0 |
You will be dealing with data that looks something like this now:
_ = elections.plot("PP_lost", cmap="binary", linewidth=.1, edgecolor="grey")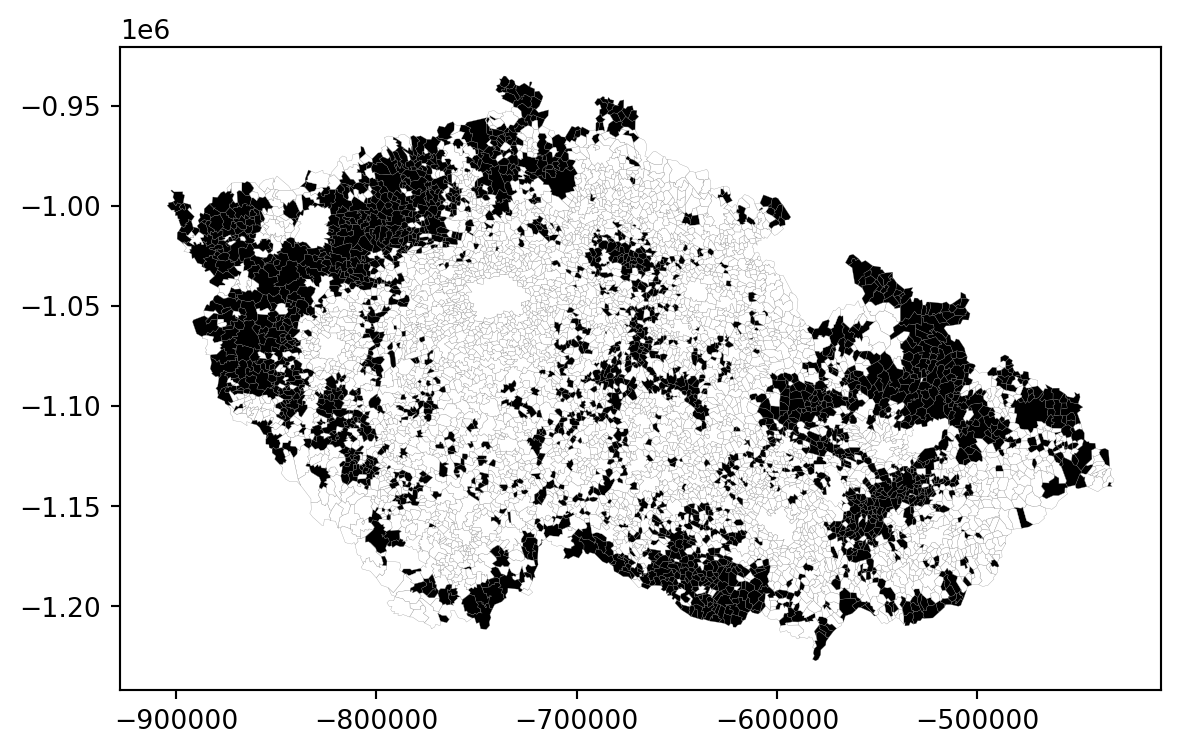
Since you are looking for spatial autocorrelation, you can already guess this will be a clear case since there are large clusters of black and white municipalities. However, your (even educated) guess is not enough. Instead, you can use the Join Count statistic. Its principle is simple. Given a checkboard with black (0) and white (1) cells, you can count how many times black is next to another black (BB), how many times white is next to white (WW) and how many times there are black-white relationships (BW). The prevalence of BB and WW indicates positive autocorrelation, while the prevalence of BW indicates a negative one. The significance is then derived from comparing how many BB, WW and BW occurrences you could expect under complete spatial randomness.
The weights for Join Counts are expected to be binary. So you could either use the original contiguity weights, which are binary by default, or transform contiguity_r to binary. You can then measure the statistics using the Join_Counts class from esda.
- 1
-
esda.Join_Countswill compute all you will need. - 2
- Pass in a Series of the (binary) variable of interest.
- 3
- And the spatial weights matrix.
The results are all stored in the jc object. You can ask for the observed number of black-black relations:
jc.bbnp.float64(3700.0)Or for white-white relations.
jc.wwnp.float64(9678.0)And the remaining black-white relations.
jc.bwnp.float64(5069.0)The total number of joins, composed of all three options summed together, is available as .J.
jc.Jnp.float64(18447.0)The key aspect of the statistic is the comparison of the number of observed BB and BW joins with that coming from simulated randomness. If the variable was purely random, the number of BB joins would be roughly:
jc.mean_bbnp.float64(2207.766766766767)And the number of BW joins would be:
jc.mean_bwnp.float64(8351.693693693695)Given the simulated values are nowhere close to the observed counts, you can assume an existence of positive spatial autocorrelation. You can also retrieve the simulated pseudo-\(p\)-values indicating significance:
jc.p_sim_bbnp.float64(0.001)Join_Counts
The Join_Counts class includes much more than these. Explore them yourself!
Moran Plot
When dealing with continuous variables, the first indication of spatial autocorrelation can be obtained using the Moran plot.The Moran Plot is a graphical way to start exploring the concept of spatial autocorrelation, and it is a good application of spatial weight matrices and the spatial lag. In essence, it is a standard scatter plot in which a given variable (area, for example) is plotted against its own spatial lag. Usually, a fitted line is added to include more information. In order to easily compare different scatter plots and spot outlier observations, it is common practice to standardise the values of the variable before computing its spatial lag and plotting it. Let’s have a look at what it looks like in this case based on the standardised values you made above.
1f, ax = plt.subplots(1, figsize=(6, 6))
sns.regplot(
x="PP_std",
y="PP_std_lag",
data=elections,
marker=".",
2 scatter_kws={"alpha": 0.2},
line_kws=dict(color="lightcoral")
)
3ax.set_aspect('equal')
plt.axvline(0, c="black", alpha=0.5)
plt.axhline(0, c="black", alpha=0.5)
4plt.text(2.3, 2.7, "High-high", fontsize=10)
plt.text(2.3, -2.7, "High-low", fontsize=10)
plt.text(-4.4, 2.7, "Low-high", fontsize=10)
plt.text(-4.4, -2.7, "Low-low", fontsize=10);- 1
-
Setup the figure (
f) and axis (ax) to allow setting the size of the figure and forcing it to be square. - 2
- Make points semi-transparent to mitigate their density.
- 3
- Ensure both x an y axes use the same scale.
- 4
- Annotate different quadrants.
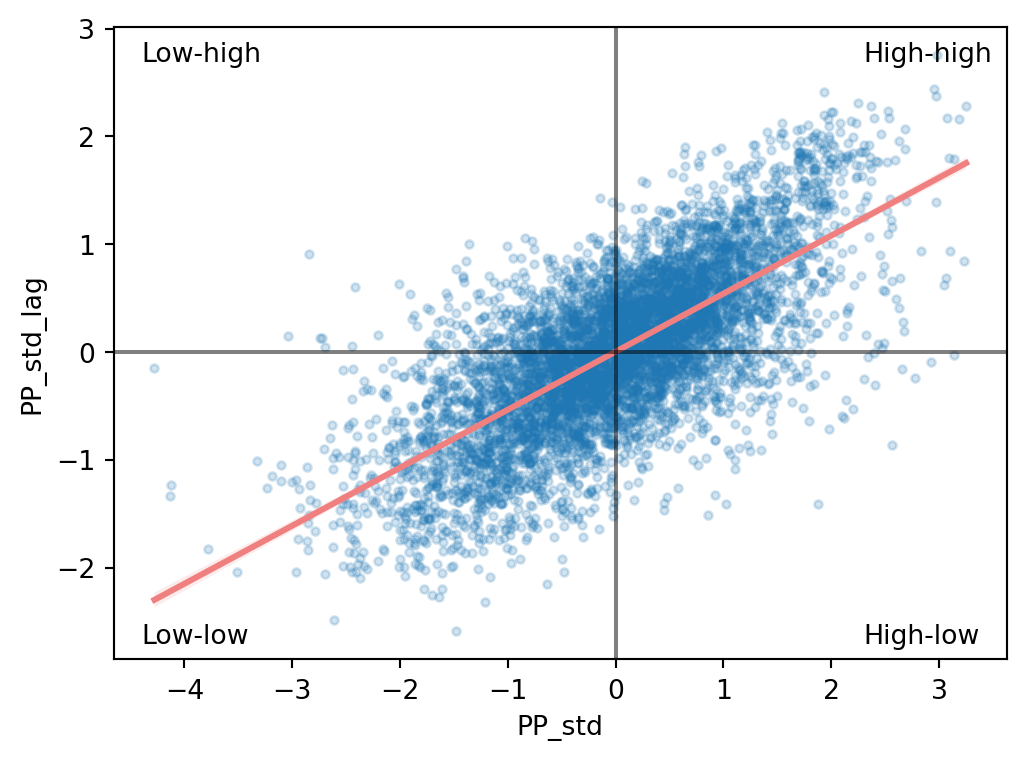
Creating a standardised Moran Plot implies that average values are centred in the plot (as they are zero when standardised), and dispersion is expressed in standard deviations, with the rule of thumb of values greater or smaller than two standard deviations being outliers. A standardised Moran Plot also partitions the space into four quadrants that represent different situations:
- High-High (HH): values above average surrounded by values above average.
- Low-Low (LL): values below average surrounded by values below average.
- High-Low (HL): values above average surrounded by values below average.
- Low-High (LH): values below average surrounded by values above average.
The figure above displays the relationship between the standardised percentage that voted for Petr Pavel ("PP_std") and its spatial lag, which, because the \(W\) that was used is row-standardized, can be interpreted as the average percentage that voted to Petr Pavel in the surrounding areas of a given municipality. In order to guide the interpretation of the plot, a linear fit is also included in the post. This line represents the best linear fit to the scatter plot or, in other words, the best way to represent the relationship between the two variables as a straight line.
The plot displays a positive relationship between both variables. This is associated with the presence of positive spatial autocorrelation: similar values tend to be located close to each other. This means that the overall trend is for high values to be close to other high values, and for low values to be surrounded by other low values. This, however, does not mean that this is only situation in the dataset: there can, of course, be particular cases where high values are surrounded by low ones, and vice versa. But it means that if you had to summarise the main pattern of the data in terms of how clustered similar values are, the best way would be to say they are positively correlated and, hence, clustered over space.
In the context of the example, this can be interpreted along the lines of: municipalities display positive spatial autocorrelation in the way they voted in the presidential elections. This means that municipalities with a high percentage of Pavel’s voters tend to be located near other municipalities where a significant share of the electorate also voted for him and vice versa.
Moran’s \(I\)
The Moran Plot is an excellent tool to explore the data and understand to which degree values are clustered over space. However, because it is a graphical device, it is sometimes hard to concisely condense its insights. For these cases, a good approach is to come up with a statistical measure that summarises the figure. This is exactly what Moran’s \(I\) is meant to do.
Very much in the same way the mean summarises a crucial element of the distribution of values in a non-spatial setting, so does Moran’s \(I\) for a spatial dataset. Continuing the comparison, you can think of the mean as a single numerical value summarising a histogram or a kernel density plot. Similarly, Moran’s \(I\) captures much of the essence of the Moran Plot. In fact, there is an even closer connection between the two: the value of Moran’s \(I\) corresponds with the slope of the linear fit overlayed on top of the Moran Plot.
In order to calculate Moran’s \(I\) in your dataset, you can call a specific function in PySAL’s esda package directly:
1mi = esda.Moran(elections['PetrPavel'], contiguity_r)- 1
- Note how you do not need to use the standardised version of the variable in this context, as you will not represent it visually.
The class esda.Moran creates an object that contains much more information than the actual statistic. If you want to retrieve the value of the statistic, you can do it this way:
mi.Inp.float64(0.5381116104224432)The other bit of information you will extract from Moran’s \(I\) relates to statistical inference: How likely is the pattern you observe in the map and Moran’s \(I\) captures in its value to be generated by an entirely random process? If you consider the same variable but shuffled its locations randomly, would you obtain a map with a similar characteristics?
The specific details of the mechanism to calculate this are beyond the scope of the session, but it is important to know that a small enough \(p\)-value associated with the Moran’s \(I\) of a map allows you to reject the hypothesis that the map is random. In other words, you can conclude that the map displays more spatial patterns than you would expect if the values had been randomly allocated to a particular location.
The most reliable \(p\)-value for Moran’s \(I\) can be found in the attribute .p_sim:
mi.p_simnp.float64(0.001)That is just 0.1%, and, by standard terms, it would be considered statistically significant. You can quickly elaborate on its intuition. What that 0.001 (or 0.1%) means that if you generated a large number of maps with the same values but randomly allocated over space, and calculated the Moran’s \(I\) statistic for each of those maps, only 0.1% of them would display a larger (absolute) value than the one you obtain from the real data and the other 99.9% of the random maps would receive a smaller (absolute) value of Moran’s \(I\). If you remember again, the value of Moran’s \(I\) can also be interpreted as the slope of the Moran Plot, what you have is that, in this case, the particular spatial arrangement of values for Pavel’s votes is more concentrated than if the values had been allocated following a completely spatially random process, hence the statistical significance.
As a first step, the global autocorrelation analysis can teach us that observations do seem to be positively correlated over space. In terms of your initial goal to find spatial structure in the attitude towards elections, this view seems to align: if the vote had no such structure; it should not show a pattern over space -technically, it would show a random one.
Correlogram
The outcome of the spatial autocorrelation assessment is heavily dependent on the spatial weights matrix that is used to represent spatial relations. It will look different for Queen contiguity and for k-nearest neighbor graph of 100 neighbors. It will look differently when using small distance band compared to a large one. Each of these is individually valid and the fact that they are different does not make one more “correct” than the other. The difference reflects the different degree of spatial similarity at different definitions of “neighbourhoods”.
This property can be used to gain insights into the spatial extent of autocorrelation and assessment of its change as we change the distance within which we consider other geometries as neighbors. For that, we use a concept of correlogram, which is similar to variogram you may know, but shows the change of the autocorrelation index depending on the change of the extent used to generate distance-based (KNN or band) weights.
Given the data used here covers the entirety of Czechia, the distances to test would need reflect such scale. An easier option is to use the KNN definition of distance.
1k = [5, 10, 25, 50, 75, 100, 250, 500, 1000]- 1
- Define options of number of nearest neighbors to test. We can leave this to the function but it defaults to 50 options which may take a while.
Fitting a correlogram happens in a single function that returns a table of autocorrelation statistics.
- 1
- Geometry needs to be represented as points.
- 2
- Variable is your array of election results as above.
- 3
- Support reflects list of values at which to compute the autocorrelation statistic.
- 4
-
Distance type can be either
"band"for distance band (in meters) or"knn"for K-nearest neighbours.
The correlogram returns a DataFrame that contains all the information you may possibly want. However, in most cases, you are interested in the actual value of the index. By default, esda.correlogram uses Moran’s \(I\), with the index being accessible as correlogram.I.
correlogram.I5 0.541311
10 0.512968
25 0.460893
50 0.410087
75 0.376964
100 0.350617
250 0.257257
500 0.182378
1000 0.099892
Name: I, dtype: float64The correlogram is then a visualisation of the curve defined by this Series.
ax = correlogram.I.plot()
ax.set_xlabel("K-nearest neighbors")
_ = ax.set_ylabel("Moran's I")
You can read from the figure that while there is a relatively high spatial autocorrelation when considering a small number of nearest neighbours, it very quickly falls down as you consider larger neighbourhoods, showcasing the spatial extent of it.
The correlogram can be used to show Moran’s \(I\) or any other autocorrelation statistic, like Geary’s \(C\) or Getis-Ord’s \(G\). You can also fit a non-parametric curve to estimate spatial autocorrelation as a function of distance, using LOWESS smoother. This can be interpreted as the correlation between observations separated by approximately the distance on the horizontal axis. See the documentation for details.
Local Spatial autocorrelation
Moran’s \(I\) is a good tool to summarise a dataset into a single value that informs about its degree of clustering. However, it is not an appropriate measure to identify areas within the map where specific values are located. In other words, Moran’s \(I\) can tell us values are clustered overall, but it will not inform us about where the clusters are. For that purpose, you need to use a local measure of spatial autocorrelation. Local measures consider every single observation in a dataset and operate on them, as opposed to on the overall data, as global measures do. Because of that, they are not good at summarising a map, but they allow you to obtain further insight.
In this session, you will consider Local Indicators of Spatial Association (LISAs), a local counterpart of global measures like Moran’s \(I\). At the core of these methods is a classification of the observations in a dataset into four groups derived from the Moran Plot: high values surrounded by high values (HH), low values nearby other low values (LL), high values among low values (HL), and vice versa (LH). Each of these groups are typically called “quadrants”. An illustration of where each of these groups falls into the Moran Plot can be seen in the Figure 1 above.
So far, you have classified each observation in the dataset depending on its value and that of its neighbours. This is only halfway into identifying areas of unusual concentration of values. To know whether each of the locations is a statistically significant cluster of a given kind, you again need to compare it with what you would expect if the data were allocated in a completely random way. After all, by definition, every observation will be of one kind or another, based on the comparison above. However, what you are interested in is whether the strength with which the values are concentrated is unusually high.
This is exactly what LISAs are designed to do. As before, a more detailed description of their statistical underpinnings is beyond the scope in this context, but you will try to shed some light on the intuition of how they go about it. The core idea is to identify cases in which the comparison between the value of an observation and the average of its neighbours is either more similar (HH, LL) or dissimilar (HL, LH) than you would expect from pure chance. The mechanism to do this is similar to the one in the global Moran’s \(I\), but applied in this case to each observation, resulting in as many statistics as original observations.
LISAs are widely used in many fields to identify clusters of values in space. They are a very useful tool that can quickly return areas in which values are concentrated and provide suggestive evidence about the processes that might be at work. For that, they have a prime place in the exploratory toolbox. Examples of contexts where LISAs can be useful include identification of spatial clusters of poverty in regions, detection of ethnic enclaves, delineation of areas of particularly high/low activity of any phenomenon, etc.
In Python, you can calculate LISAs in a very streamlined way thanks to esda:
lisa = esda.Moran_Local(elections['PetrPavel'], contiguity_r)All you need to pass is the variable of interest -the percentage of Pavel’s votes- and the spatial weights that describe the neighbourhood relations between the different observation that make up the dataset.
Because of their very nature, looking at the numerical result of LISAs is not always the most useful way to exploit all the information they can provide. Remember that you are calculating a statistic for every observation in the data, so it will be difficult to extract any meaningful pattern if you have many of them. Instead, what is typically done is to create a map, a cluster map as it is usually called, that extracts the significant observations (those that are highly unlikely to have come from pure chance) and plots them with a specific col or depending on their quadrant category.
All of the needed pieces are contained inside the lisa object you have created above. But, to make the map-making more straightforward, it is convenient to pull them out and insert them in the main data table, elections:
1elections['cluster'] = lisa.get_cluster_labels(crit_value=0.05)
elections.head()- 1
-
Use
lisa.p_sim < 0.05as a critical values.
| nationalCode | PetrPavel | AndrejBabis | sourceOfName | geometry | PP_lag | PP_std | PP_std_lag | PP_lost | cluster | |
|---|---|---|---|---|---|---|---|---|---|---|
| name | ||||||||||
| Želechovice nad Dřevnicí | 500011 | 61.73 | 38.26 | Český úřad zeměměřický a katastrální | MULTIPOLYGON (((-518835.63 -1170505.52, -51790... | 63.431667 | 0.678189 | 0.826837 | 0 | High-High |
| Petrov nad Desnou | 500020 | 49.07 | 50.92 | Český úřad zeměměřický a katastrální | MULTIPOLYGON (((-559207.18 -1075123.25, -55624... | 51.467500 | -0.427720 | -0.218287 | 1 | Insignificant |
| Libhošť | 500046 | 47.78 | 52.21 | Český úřad zeměměřický a katastrální | MULTIPOLYGON (((-486502.29 -1123694.06, -48717... | 54.154000 | -0.540407 | 0.016391 | 1 | Insignificant |
| Krhová | 500062 | 58.79 | 41.20 | Český úřad zeměměřický a katastrální | MULTIPOLYGON (((-494514.83 -1136457.23, -49539... | 57.782500 | 0.421366 | 0.333357 | 0 | Insignificant |
| Poličná | 500071 | 58.20 | 41.79 | Český úřad zeměměřický a katastrální | MULTIPOLYGON (((-499678.51 -1143457.52, -49799... | 54.198333 | 0.369827 | 0.020263 | 0 | Insignificant |
Similarly as with global Moran’s \(I\), esda is automatically computing a \(p\)-value for each LISA. Because not every observation represents a statistically significant one, you want to identify those with a \(p\)-value small enough that it rules out the possibility of obtaining a similar situation from pure chance. Following a similar reasoning as with global Moran’s \(I\), you select 5% as the threshold for statistical significance.
You can quickly map these results using the explore() method.
- 1
-
lisadoes not save geometry so you need to pass the original GeoDataFrame as a source of geometric information. - 2
- You can specify a custom threshold of significance.
The same map can be also plotted statically:
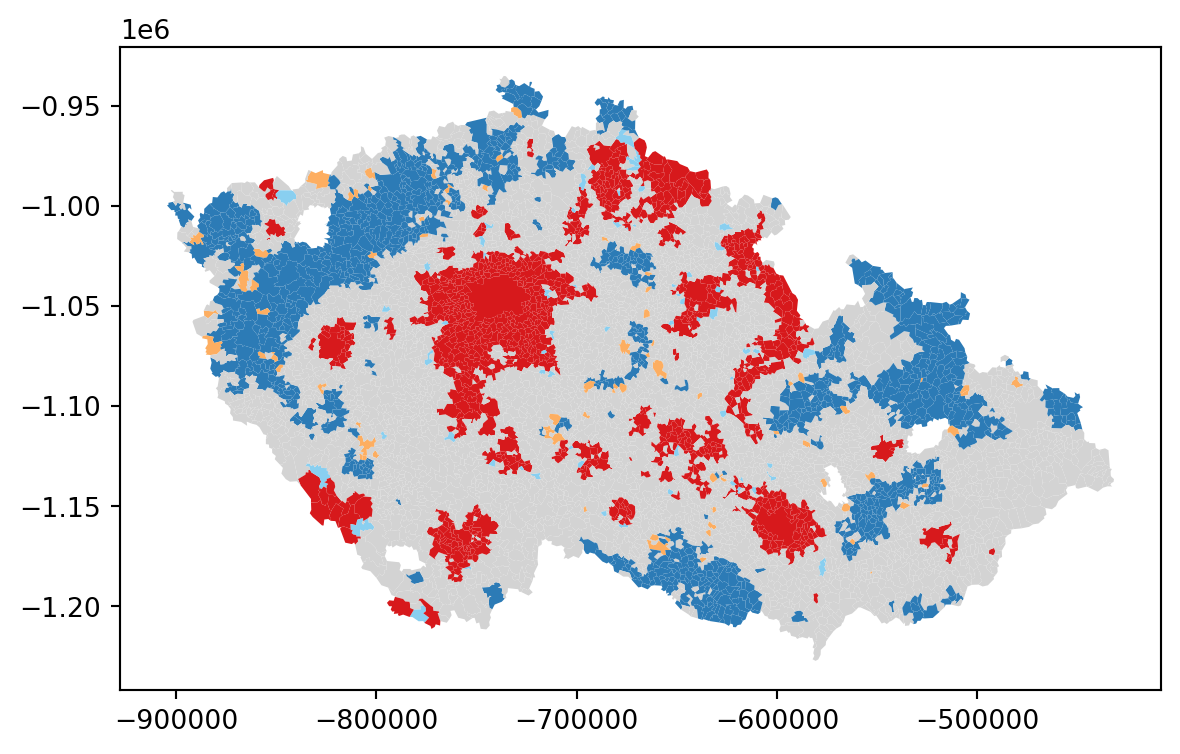
_ = lisa.plot(
elections,
crit_value=0.05,
)
You can also use use the plot_scatter() method to get a Moran Plot linking the clusters to the scatterplot.
_ = lisa.plot_scatter()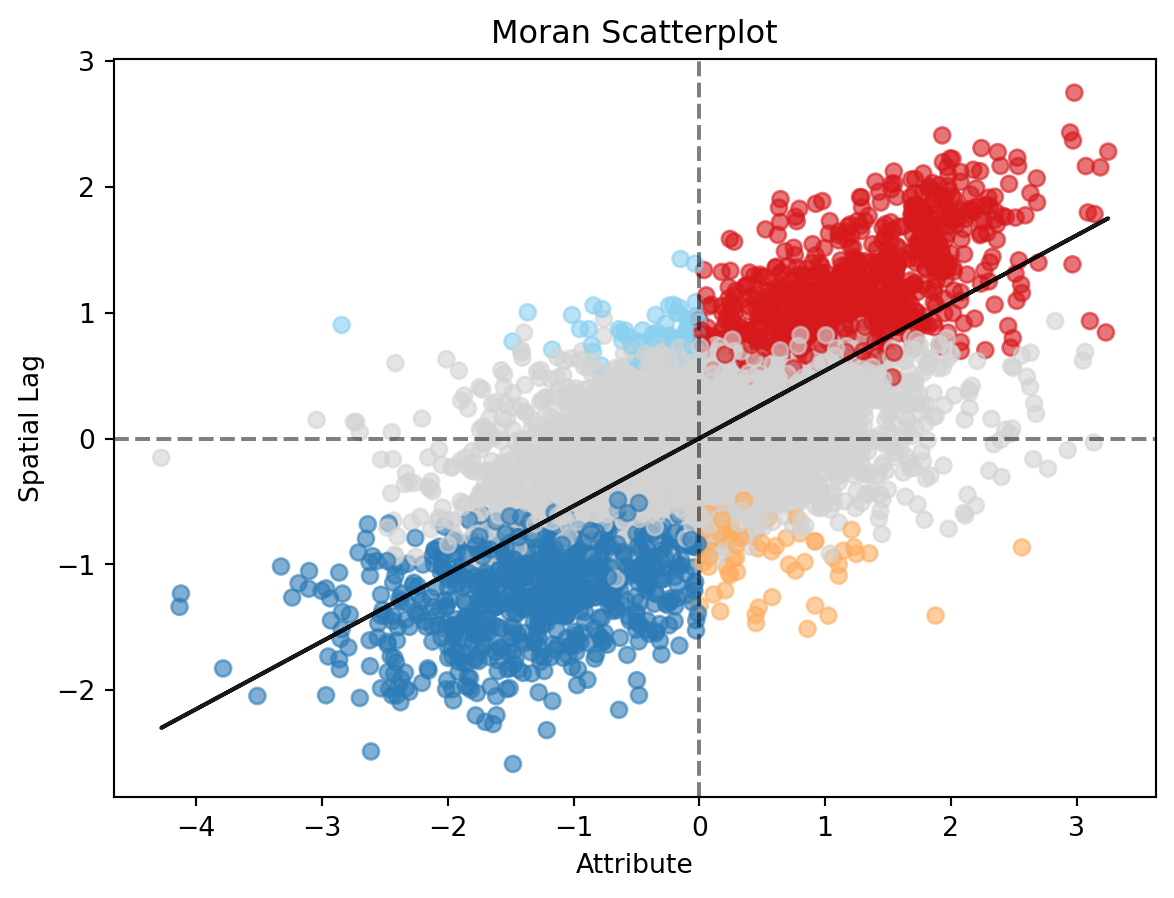
If you want to have more control over what is being displayed and how each component is presented, you can “cook” the plot by hand. The same will apply to interactive maps:
f, ax = plt.subplots(1, figsize=(6, 6))
elections.loc[elections["cluster"] == "Insignificant"].plot(ax=ax, color="lightgrey")
elections.loc[(elections["cluster"] == "High-High")].plot(ax=ax, color="#d7191c")
elections.loc[(elections["cluster"] == "Low-Low")].plot(ax=ax, color="#2c7bb6")
elections.loc[(elections["cluster"] == "Low-High")].plot(ax=ax, color="#abd9e9")
elections.loc[(elections["cluster"] == "High-Low")].plot(ax=ax, color="#fdae61");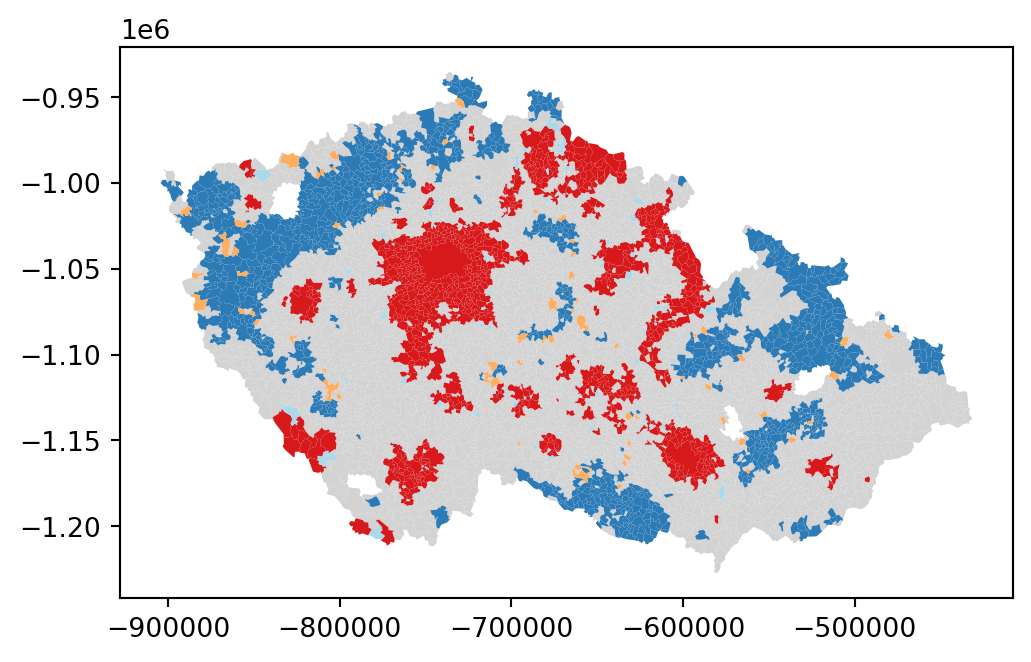
The map above displays the LISA results of the presidential elections. In bright red, you find those municipalities with an unusual concentration of high levels of Pavel’s voters also surrounded by high levels of his voters. This corresponds with areas in the Prague Metropolitan region, around other large cities like Pilsen or Brno and some other areas. On the other hand, areas in the dark blue voted against Pavel, similarly to their surrounding municipalities. In orange, you find the first type of spatial outliers. These are areas with high Pavel’s gain but surrounded by areas voting for Babiš (e.g. Mariánské Lázně). Finally, in light blue, you find the other type of spatial outlier: municipalities with low Pavel’s support surrounded by other municipalities with high support.
The substantive interpretation of a LISA map needs to relate its output to the original intention of the analyst who created the map. In this case, your original idea was to explore the spatial structure of support of Petr Pavel. The LISA proves a fairly useful tool in this context. Comparing the LISA map above with the choropleth you started with, you can interpret the LISA as a “simplification” of the detailed but perhaps too complicated picture in the choropleth that focuses the reader’s attention to the areas that display a particularly high concentration of (dis)similar values, helping the spatial structure of the vote emerge more explicitly. The result of this highlights the relevance that the cities had in voting for Pavel, as well as the regions of the map where there was a lot less excitement about him.
Other options
Join counts and Moran’s methods are not the only ways of computing spatial autocorrelation. esda offers way more, including Geary’s \(C\), Getis-Ord \(G\), which can both be measured as global or local statistics, and other methods, exposed in a similar way as those you have used today.
- Have a look at the chapters Global Spatial Autocorrelation and Local Spatial Autocorrelation from the Geographic Data Science with Python by Rey, Arribas-Bel, and Wolf (2023) for more details and some other extensions.
Acknowledgements
This section is derived from A Course on Geographic Data Science by Arribas-Bel (2019), licensed under CC-BY-SA 4.0. The code was updated to use the new libpysal.graph module instead of libpysal.weights. The text was slightly adapted to accommodate a different dataset, the module change, and the inclusion of Join counts.