
Space as math
How to include space in statistics?
We need its mathematical representation
geometries are not
graphs are
What is a graph?
a data structure that consists of a set of objects called nodes and a set of connections between them called edges
Matrix
\[ \begin{array}{cccc} 0 & w_{12} & \dots & w_{1N} \\ w_{21} & \ddots & w_{ij} & \vdots \\ \vdots & w_{ji} & 0 & \vdots \\ w_{N1} & \dots & \dots & 0 \end{array} \]
Matrix
\[ \begin{array}{cccc} 0 & 1 & 0 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array} \]
mathematical structure capturing spatial relationships
What is a neighbour?
it depends
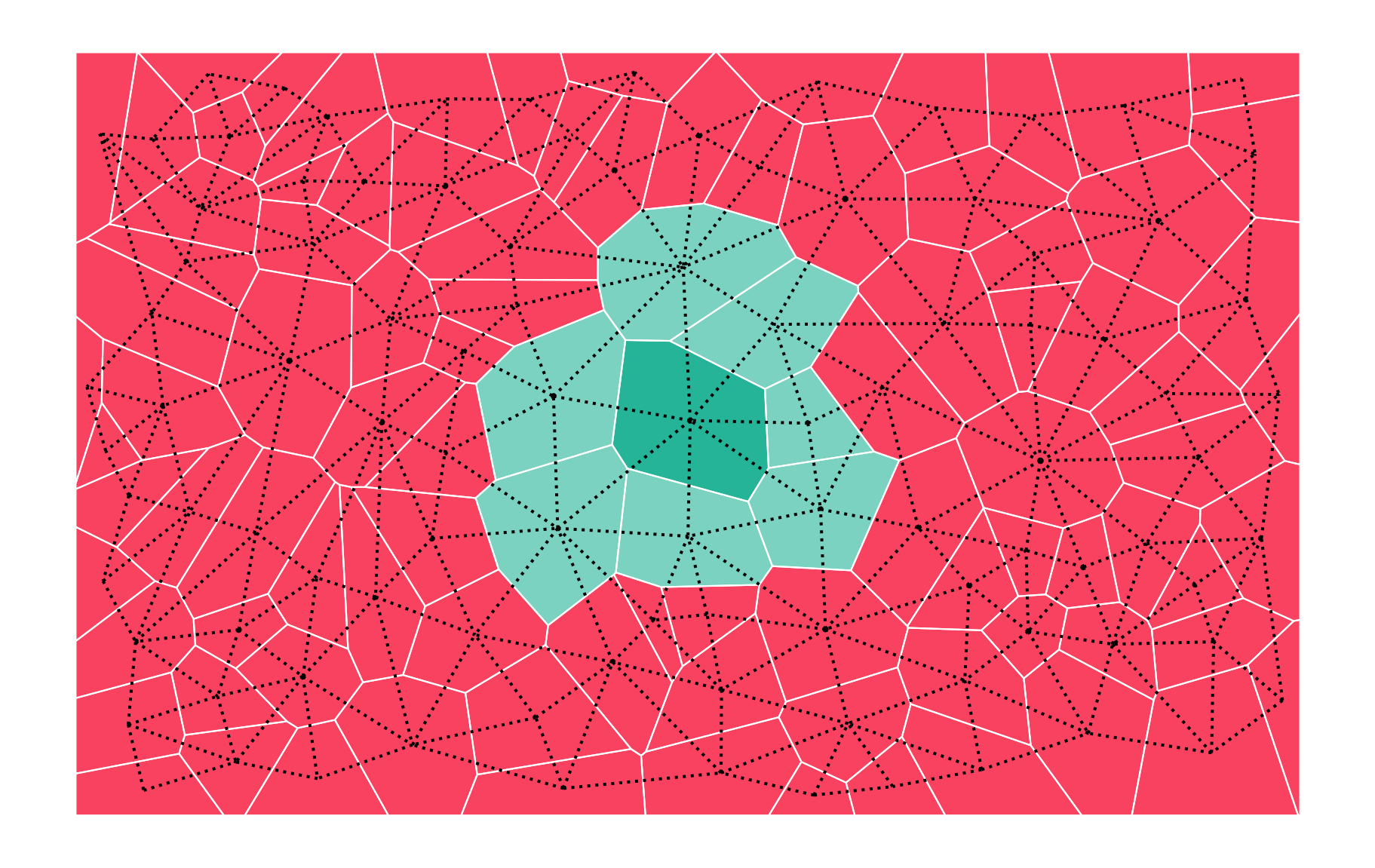
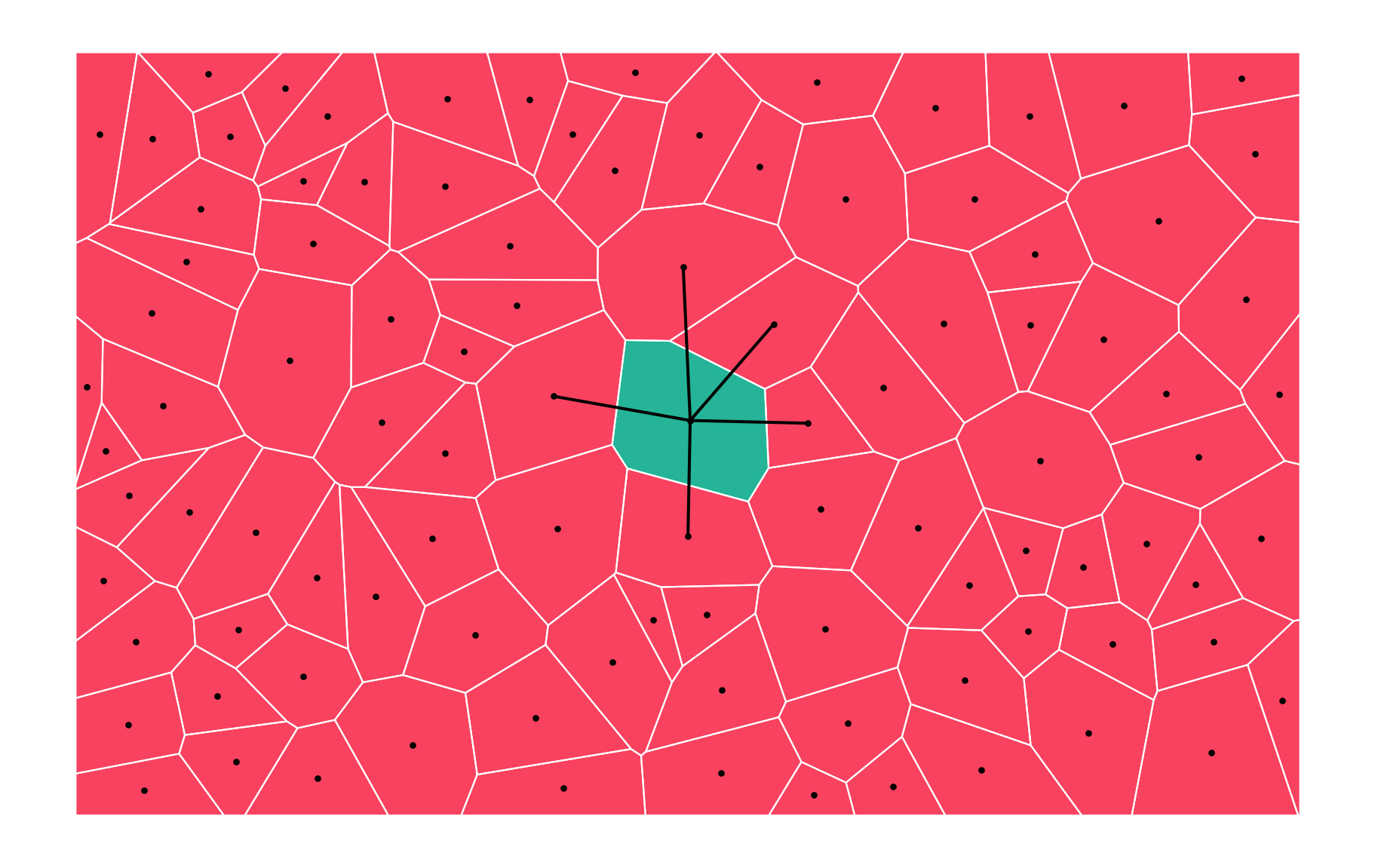
Contiguity
Two geometries are considered neighbours if they share at least one vertex (queen contiguity) or one edge (rook contiguity).



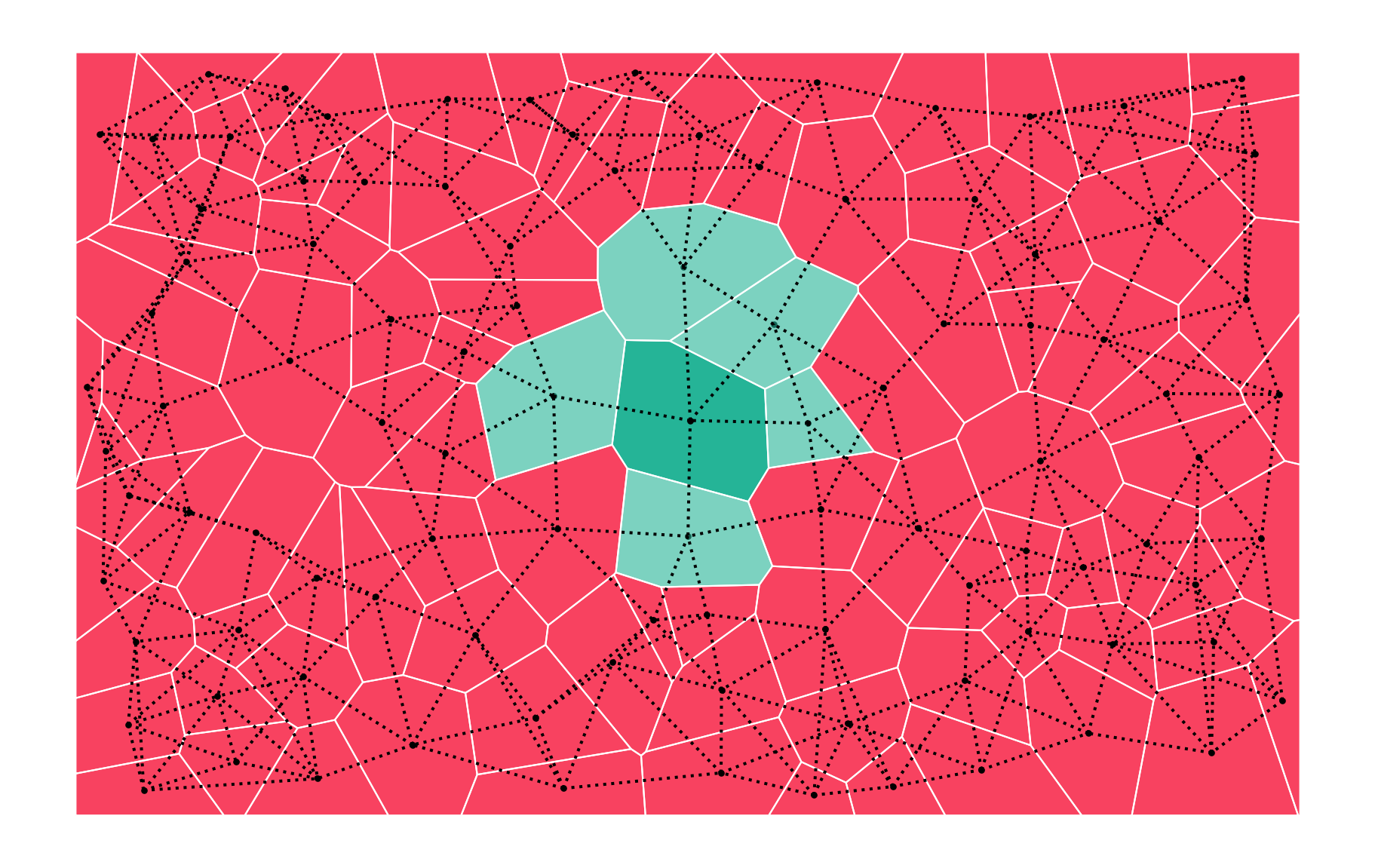
Distance
Two geometries are considered neighbours if they lie within a set threshold from each other
Distance band
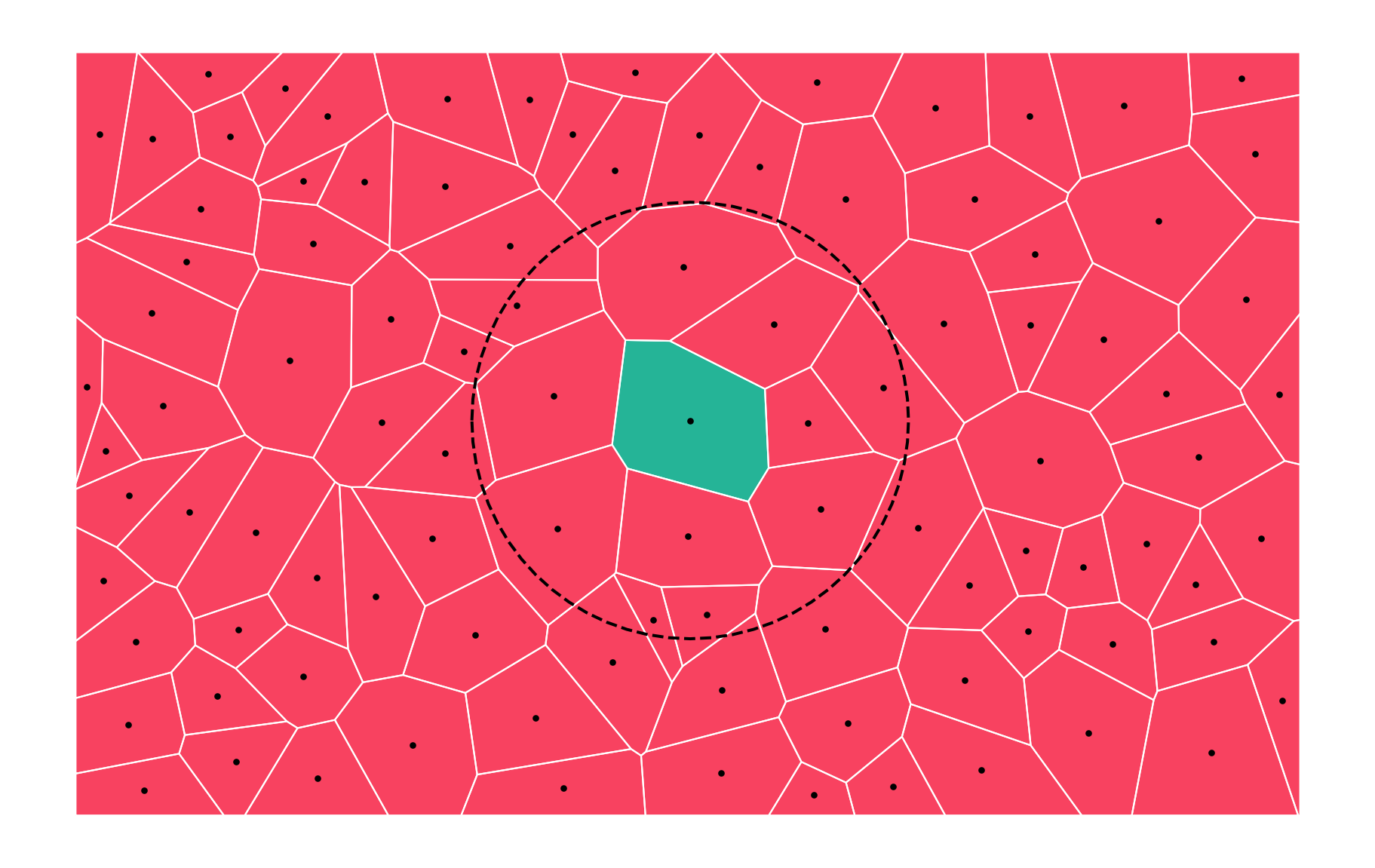

Distance
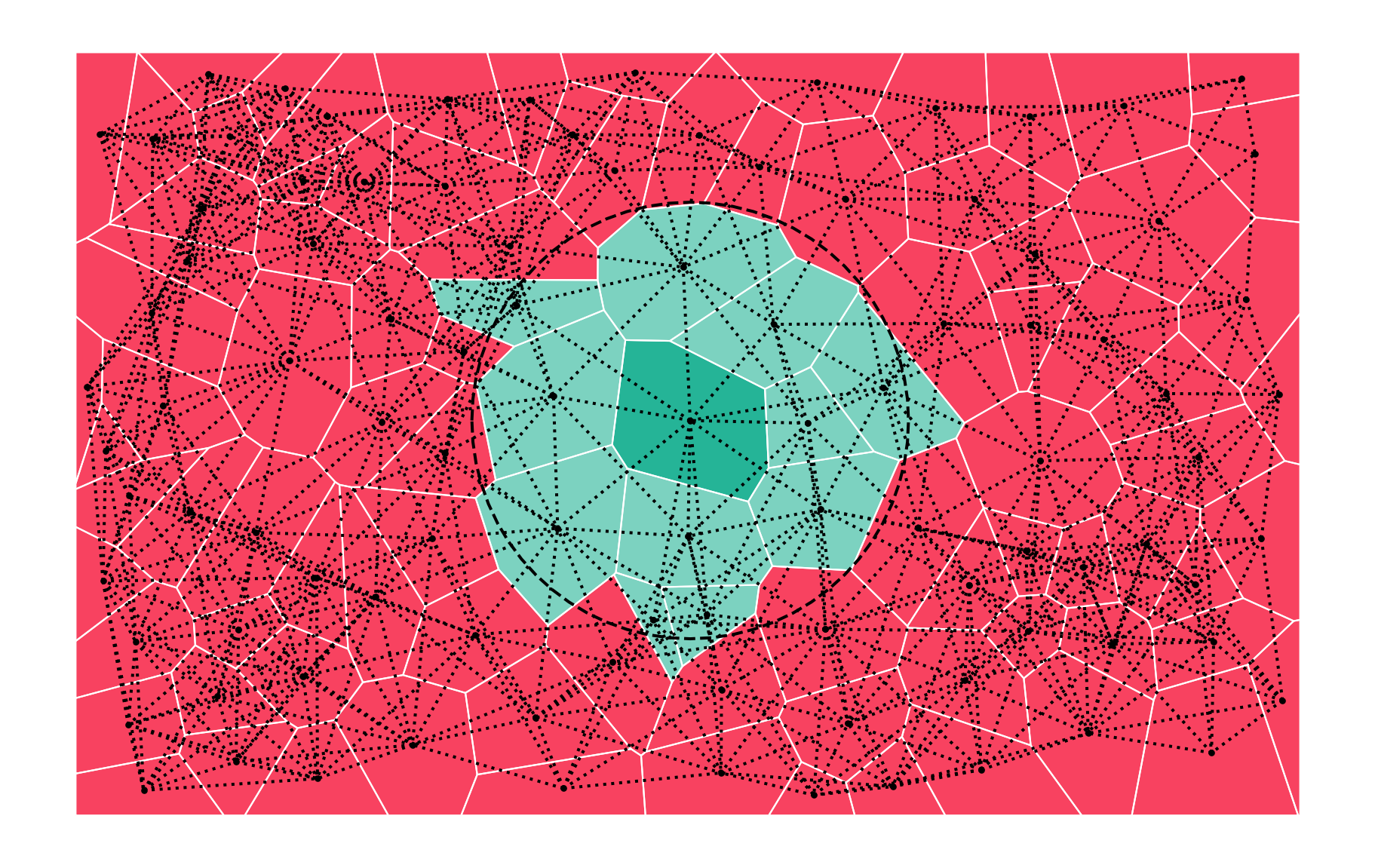
A geometry is considered a neighbour if it is no further than K-1 others
K-nearest neighbour

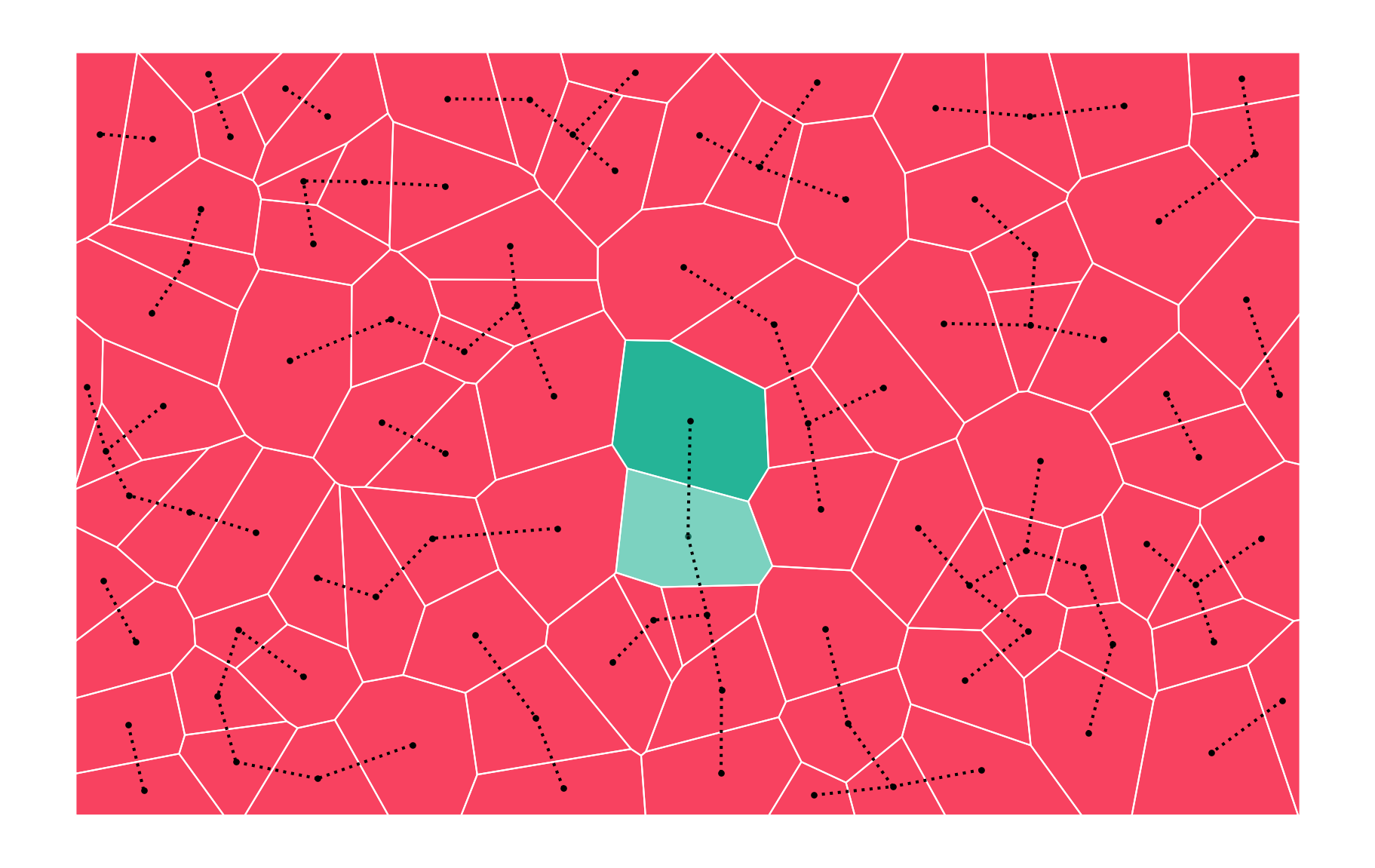

Block contiguity/regions
Two geometries are considered neighbours if they belong to the same group
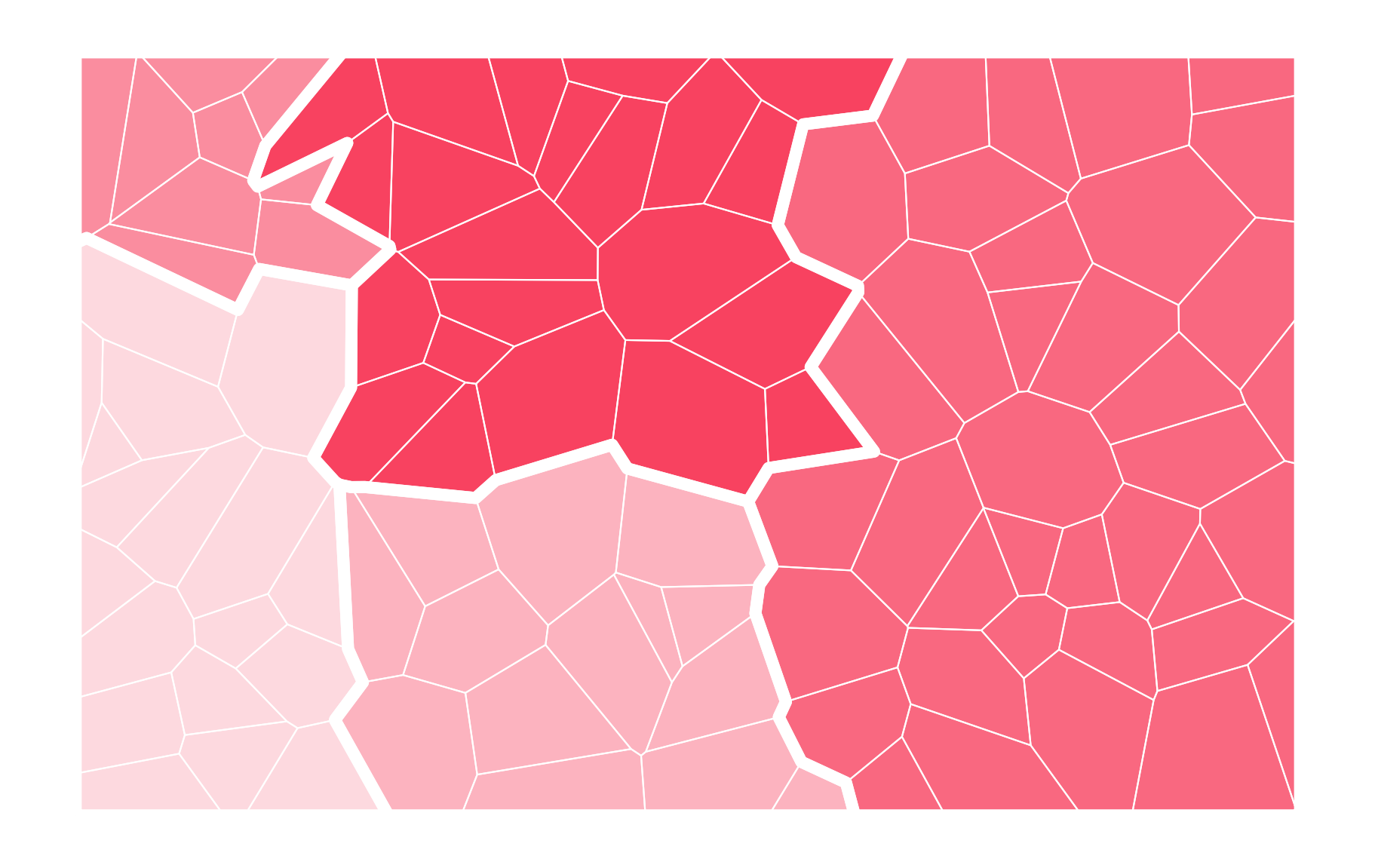
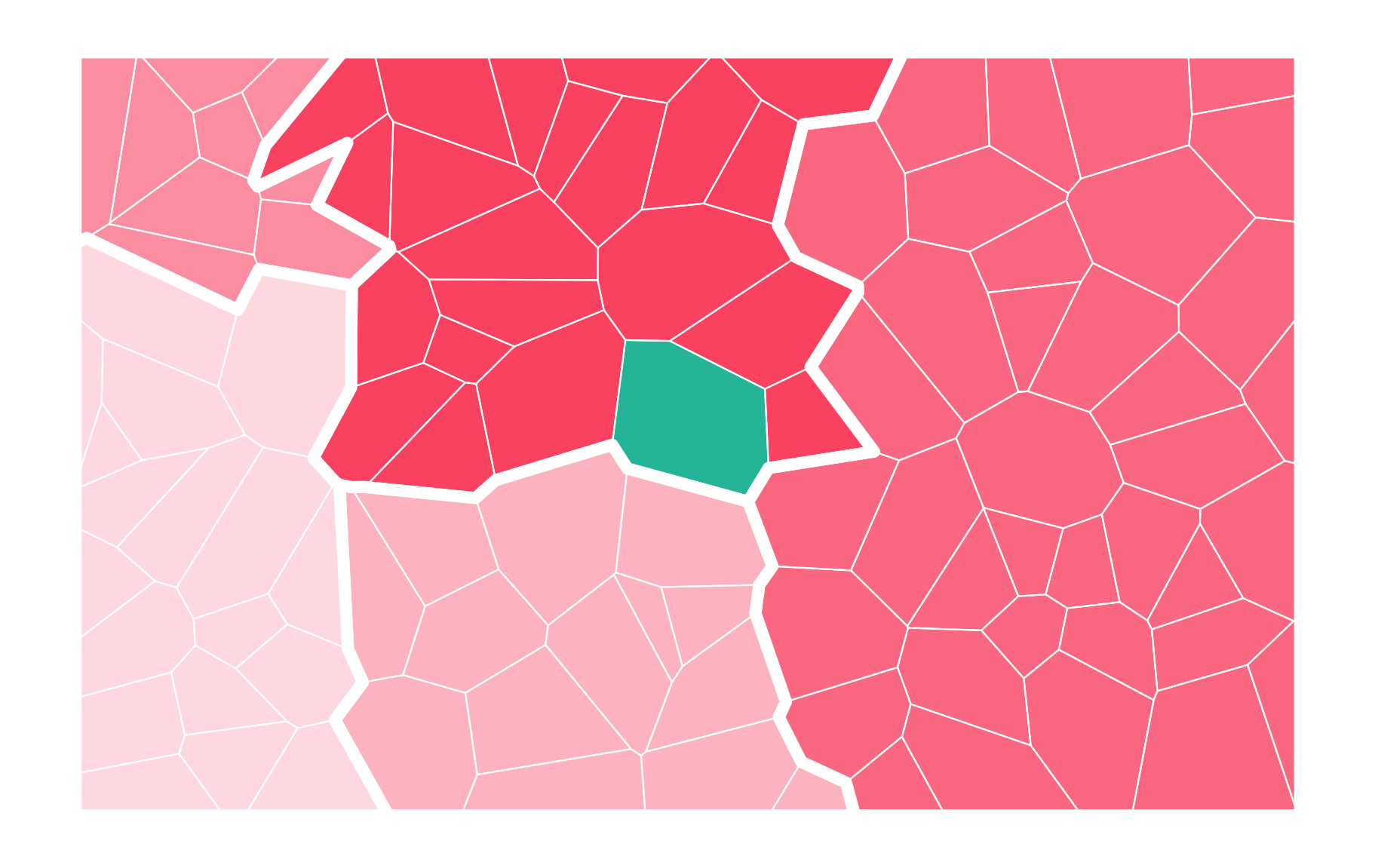
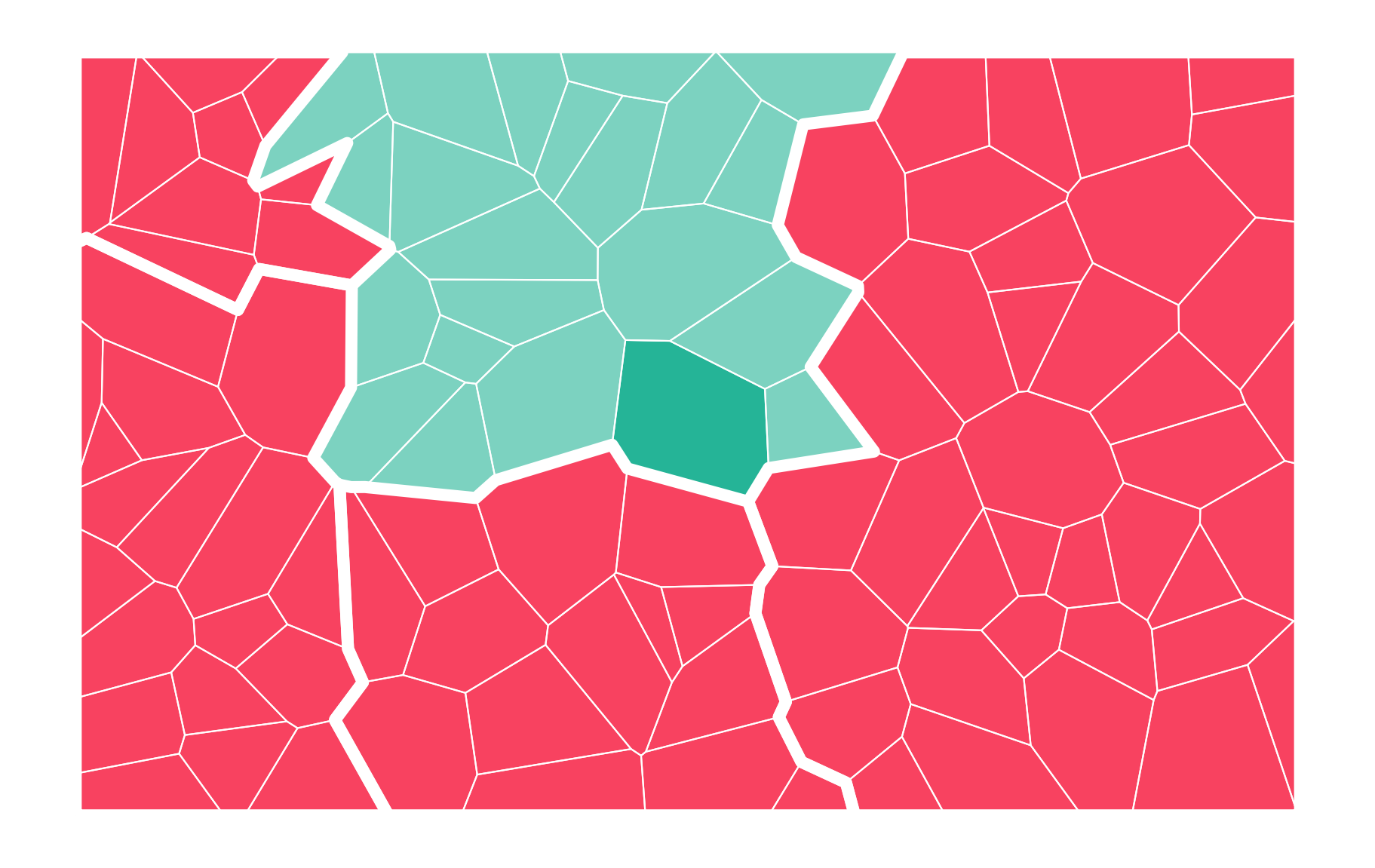


Graph routines
Order of contiguity




Component analysis
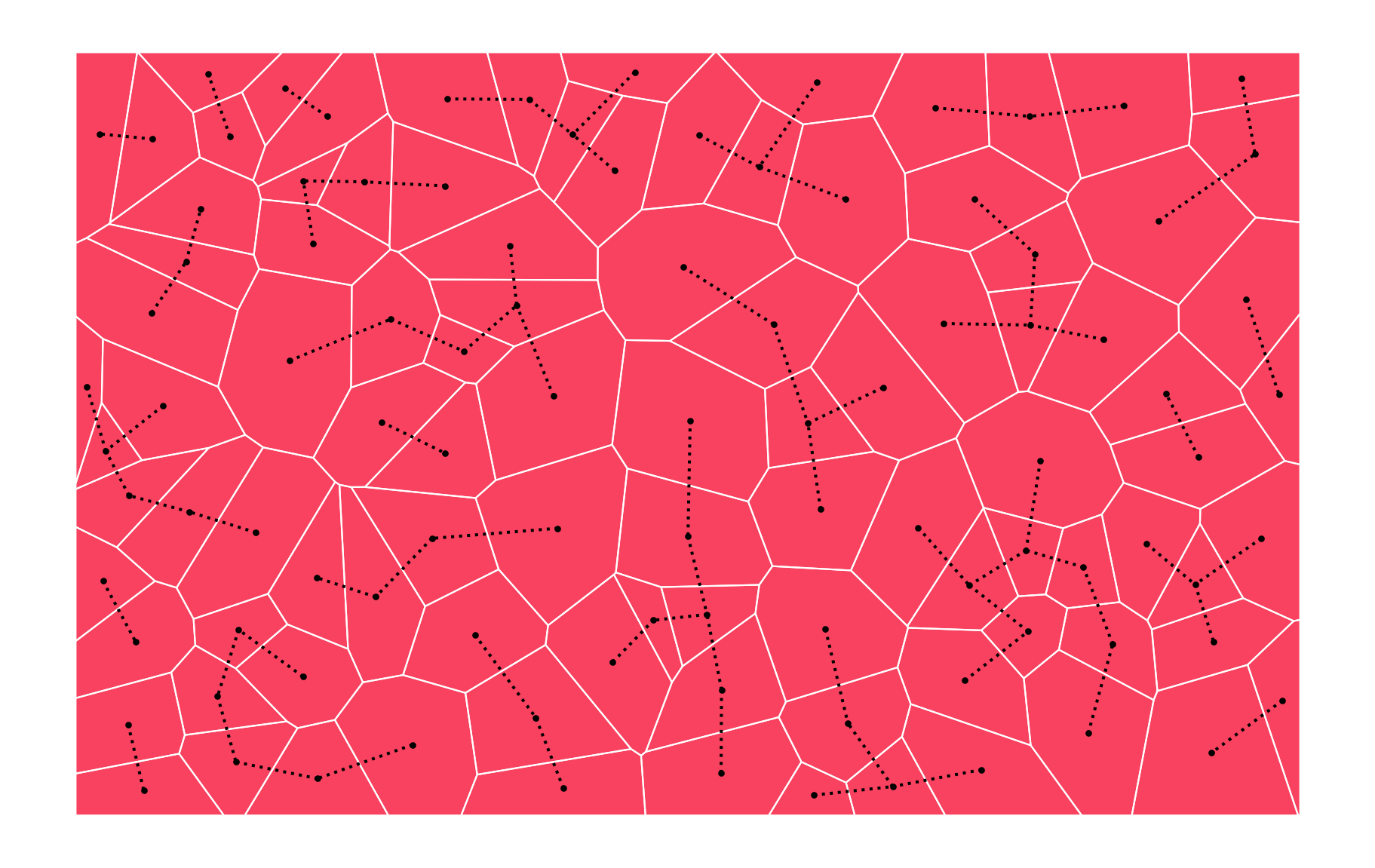
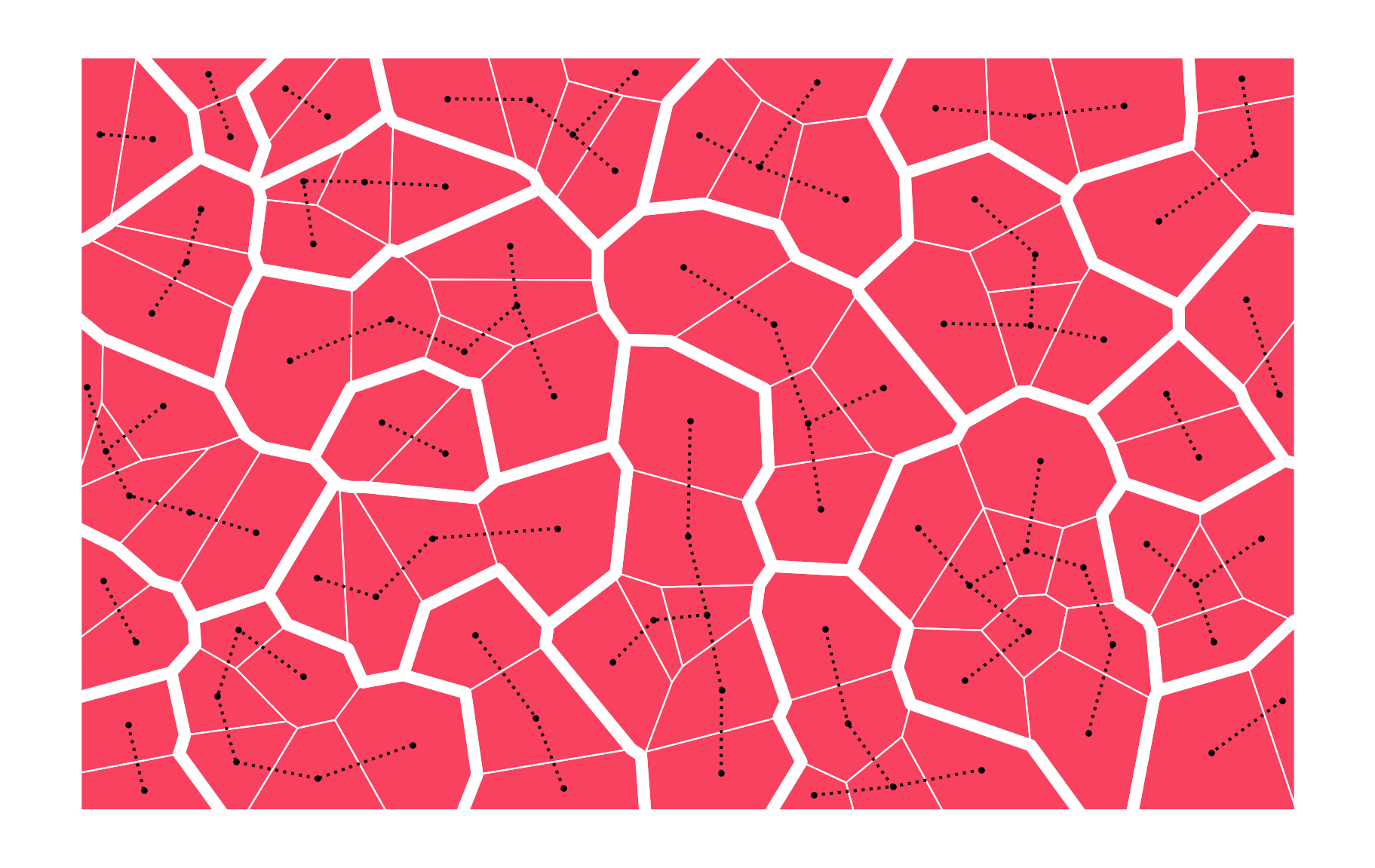
Weights are not always binary


from libpysal import graph