Relationship and prediction

Linear regression

\[y_{i}=\alpha+\beta _{1}\ x_{i1}+\beta _{2}\ x_{i2}+\cdots +\beta _{p}\ x_{ip}+\varepsilon _{i}\]

\[y_{i}=\alpha+\beta _{1}\ x_{i1}+\beta _{2}\ x_{i2}+\cdots +\beta _{p}\ x_{ip}+\varepsilon _{i}\]

\(\alpha\) = constant

\(x_{1}\) = value of a variable \(1\)

\(x_{2}\) = value of a variable \(2\)

\(\beta\) = regression coefficient

\(\varepsilon\) = error

Prediction

Relationship or effect

Assumptions

Linearity

Dependent variable is assumed to be a linear combination of independent variables

Weak exogeneity

Independent variables are assumed to contain no error

Constant variance

Variance of errors does not depend on the value of the dependent variable

Independence of errors

Residuals are not correlated with independent variables

No perfect multicollinearity

Independent variables are not perfectly multicollinear

Evaluation

\(R^2\)

Coefficient of determination

Variance of dependent that can be explained by independent

0…1

\(\beta\)

Regression coefficient

Captures the relationship between the dependent variable and independent variable

Each \(\beta\) has a \(p\) value

Residuals

\(\varepsilon\)

The error

Deviation of the prediction from the observation

Spatial evaluation

Spatial dimension of residuals

Spatial autocorrelation means a problem

Dependent variable is spatially heterogeneous

The relationship between \(\alpha\), dependent and independent variables varies across space

Spatial heterogeneity

Spatially dependent \(\alpha\)

Spatially dependent \(\beta\)

Spatially dependent \(\alpha\)

Spatial fixed effects

Spatially explicit (categorical) variable accounting for regional differences

Spatially dependent \(\beta\)

Spatial regimes

All \(\alpha\) and \(\beta\) coefficients can vary geographically

Spatially explicit (categorical) variable accounting for regional differences

Spatial dependence

configuration matters

Inlcusion of spatially lagged variables in the model

Lag of independent variables

Lag of dependent variable (violates the OLS assumptions)

Lag of error (violates the OLS assumptions)

Geographically weighted regression

single model across space is too restrictive

GWR

A system of smaller, geographically delimited regressions

Accounts for both spatial heterogeneity and spatial dependence

Spatial kernel function

Kernel type

Kernel size

Kernel shape

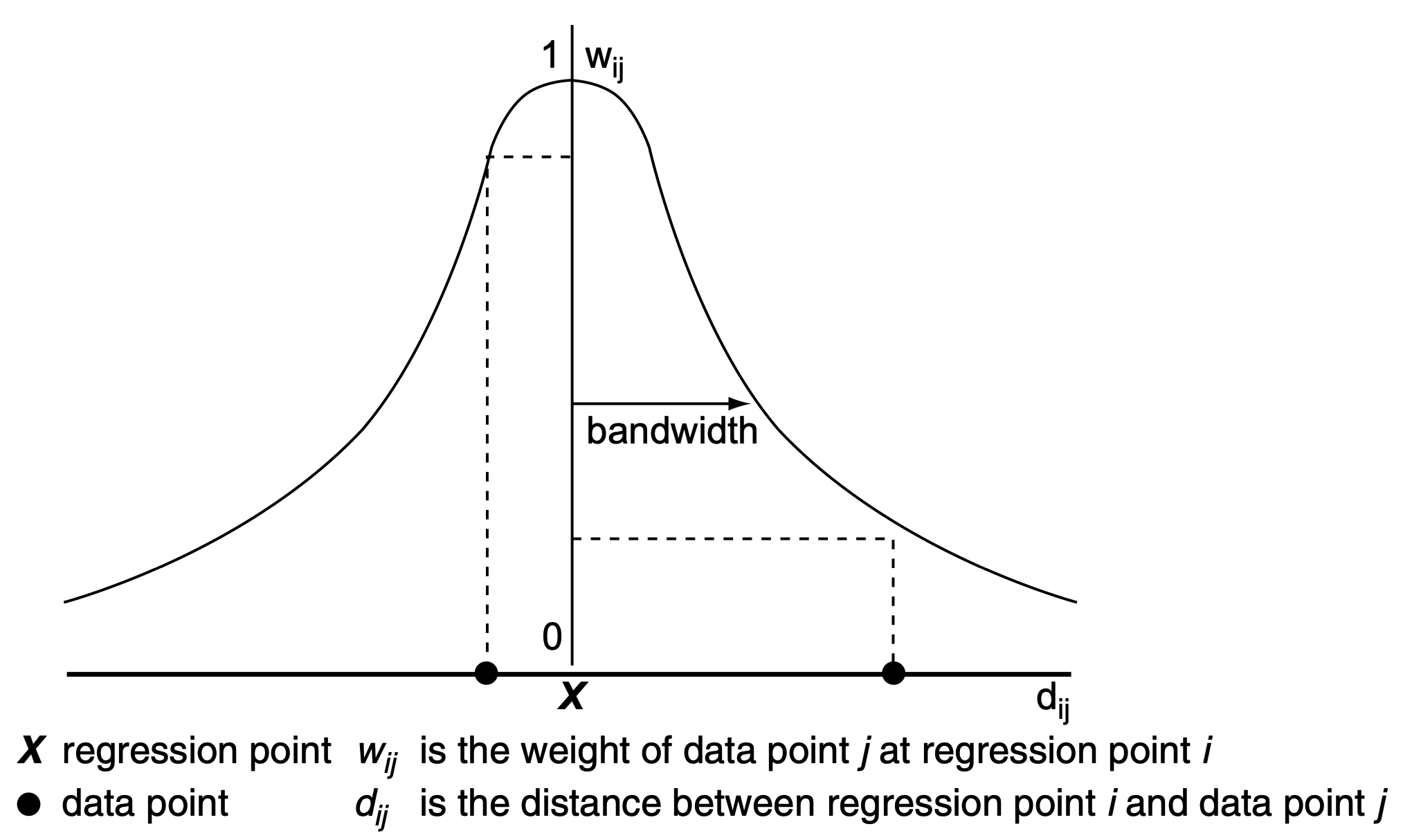
Illustration of a kernel by Fotheringham et al. (2002, p.44)

Evaluation

\(R^2\)

Coefficient of determination

Variance of dependent that can be explained by independent

0…1

Global metric

Local metric per geometry

\(\beta\)

Regression coefficient

Captures the relationship between the dependent variable and independent variable

Estimation of \(\beta\) per geometry

Significance based on \(t\) value and a critical \(t\) value

Residuals

\(\varepsilon\)

The error

Deviation of the prediction from the observation

Multiscale geographically weighted regression

Extension where each variable can have its own kernel bandwidth

Limits

(M)GWR is computationally expensive and does not scale well

Use with caution

import statsmodels
import mgwr